NavCalc solves for Course to Steer (CtS) when given a desired Heading, Boat Speed, and Current Set (direction) and Drift (velocity), and it does so using some fairly simple math.
This post goes into the details.
Traditional Chart Navigation
In Navigation class, they teach us how to solve for CtS using traditional paper charts, dividers, and a plotter. Let’s go through an example using a short trip across the San Francisco Bay from Sausalito (A) to Aquatic Park (Z). Let’s say we’re going on August 18th, 2022 at 4pm, and our boat sails at 6 knots.
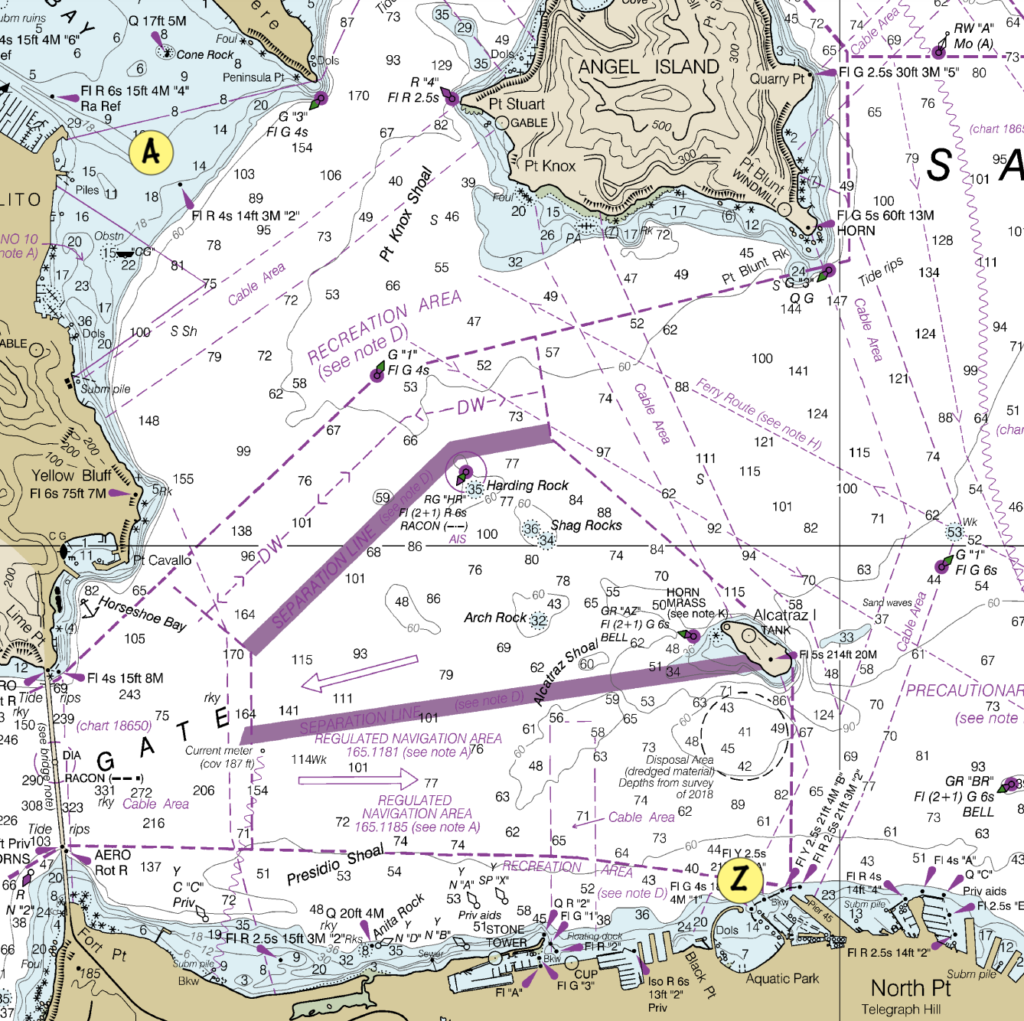
Note that these drawings are not to scale, just approximate.
Draw the Track
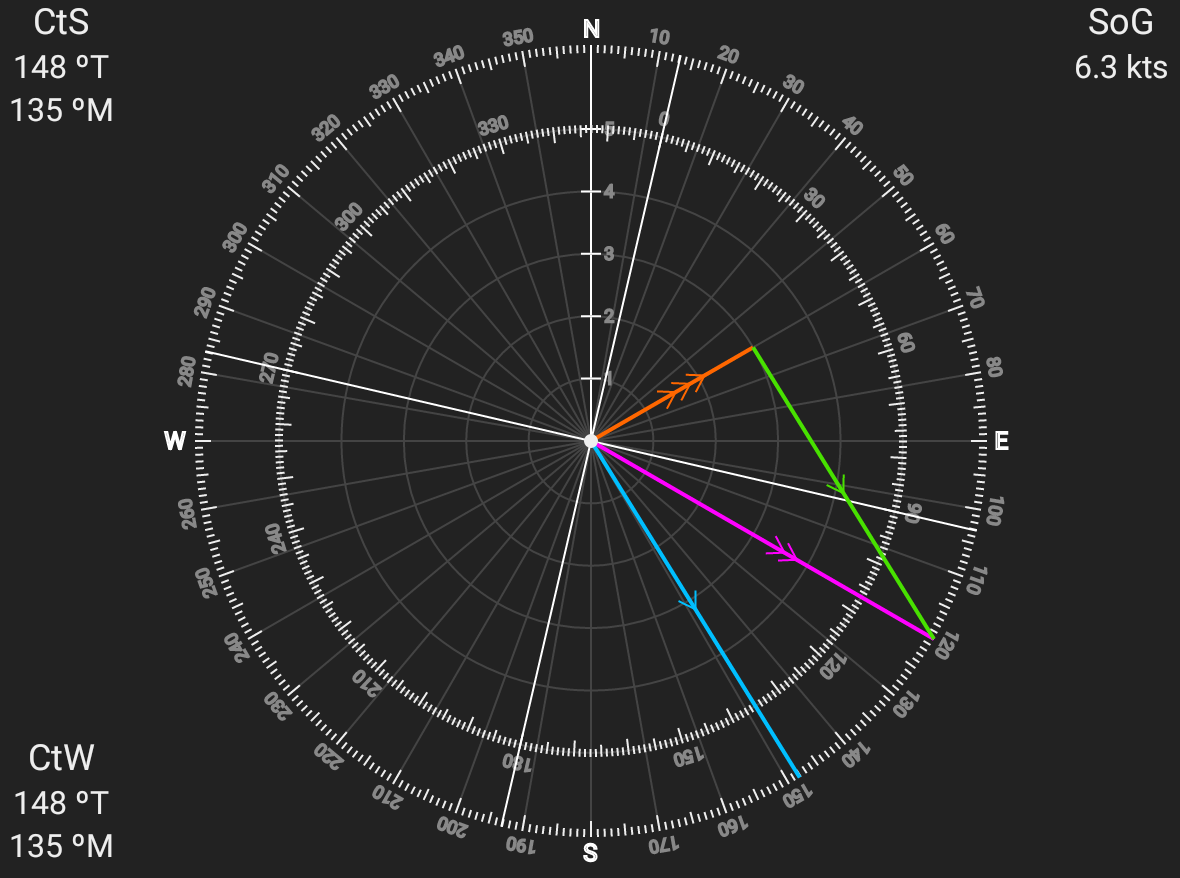
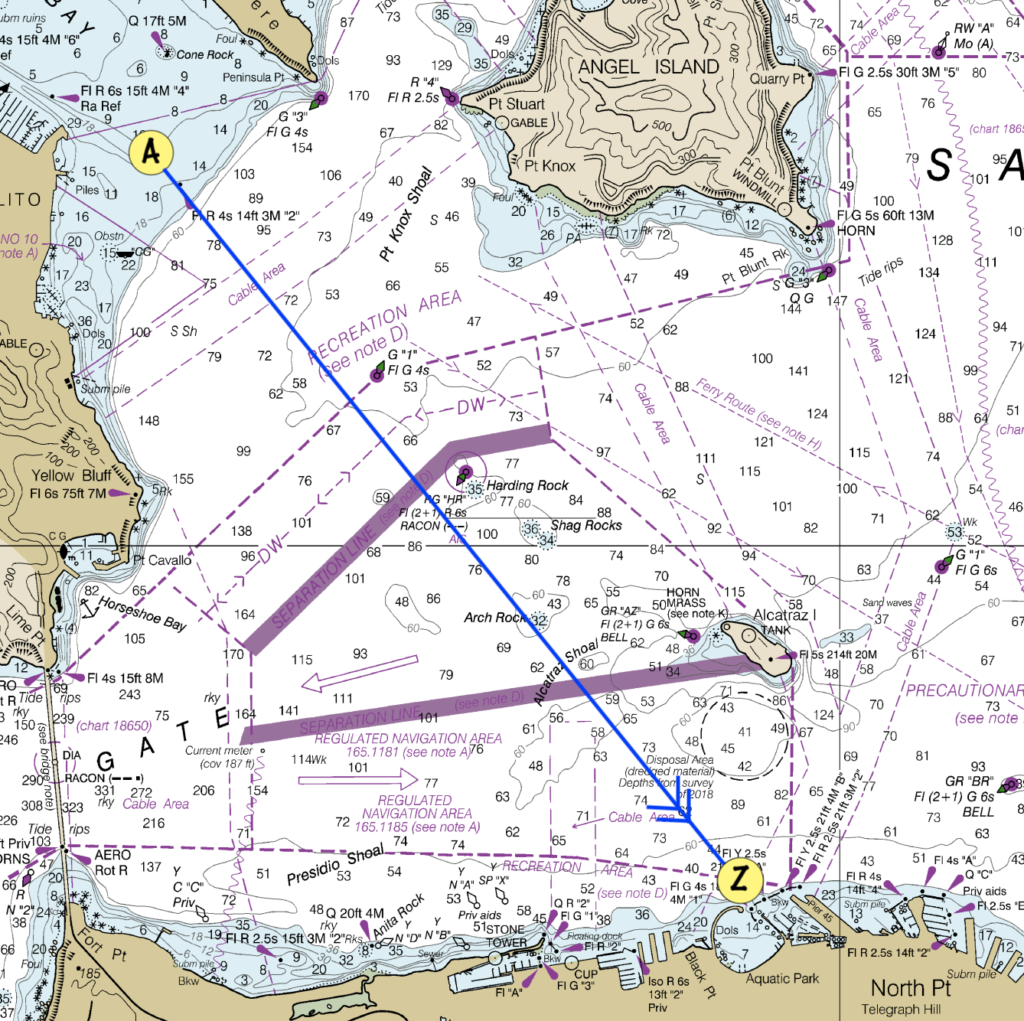
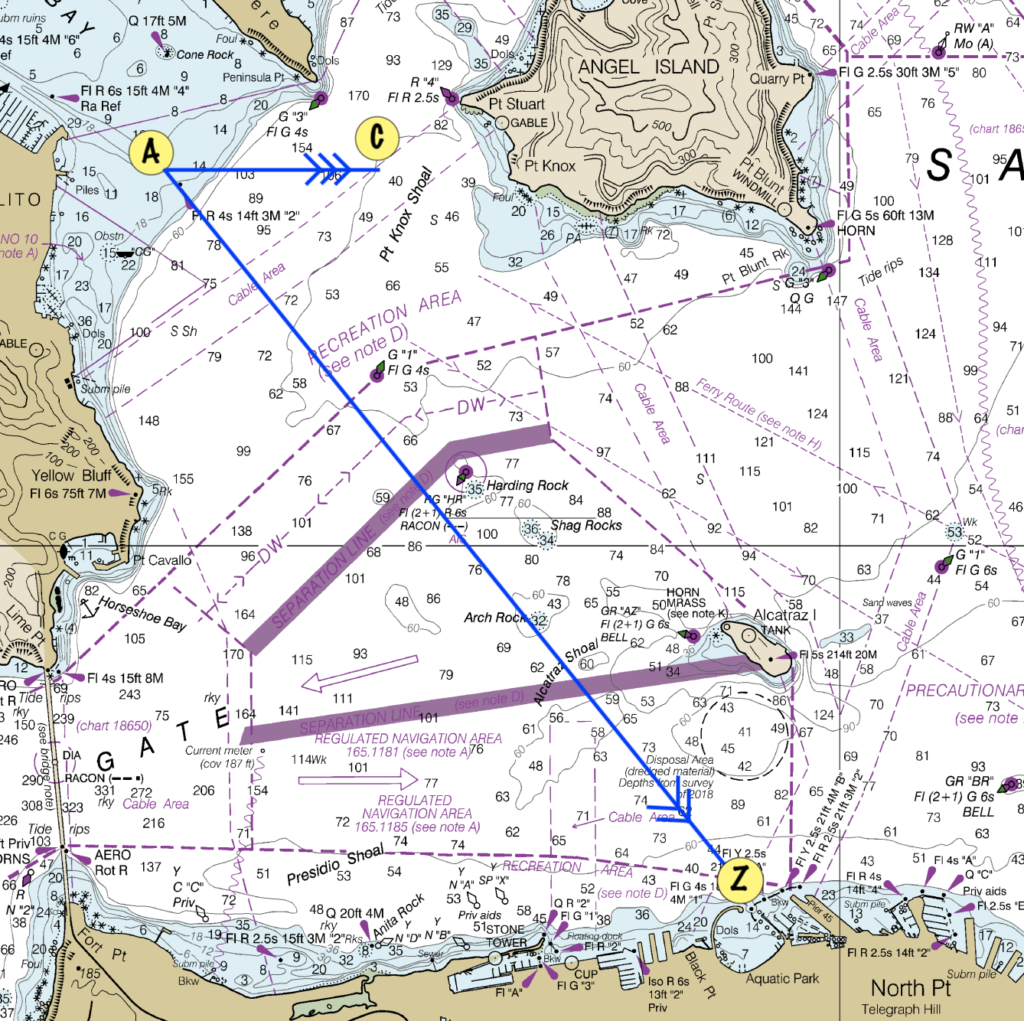
The Track is the line from where we are to where we want to be. We use a plotter to transfer that line to the compass rose on the chart to get our heading. We mark the track with two arrows.
In our example, we measure our track’s heading at 134ºT.
Draw the Current
Next, we look up the currents along our track for the date and time that we’ll be sailing. We can get these from a Tide Book or from NOAA’s handy online service. Current information will include set (direction of the current) and drift (velocity of the current in knots).
We draw a line for the current; specifically, where the current will move us in one unit of time. The current line will start at our starting point, point in the direction of the current’s set, and have a length equal to the current’s drift (since that’s how far the current will move us in one hour). We measure the length using dividers, then draw the current line and mark it with three arrows.
For our example, we’ll use the current station at “Point Cavallo, 1.3 miles east”. We see that on the day we’re going (8/18/2022) there will be a maximum flood current of 2.38 knots at 87ºT at 4:08pm, which is right when we’ll be crossing. We decide to divide boat and current speed by four in order to keep all the lines from getting too big. As long as we divide current drift and boat speed by the same constant, everything works out, so we just pick a constant that makes the lines fit nicely on the chart.
So, dividing the current drift of 2.38 knots by 4 gives us a line length of about 0.6nm.
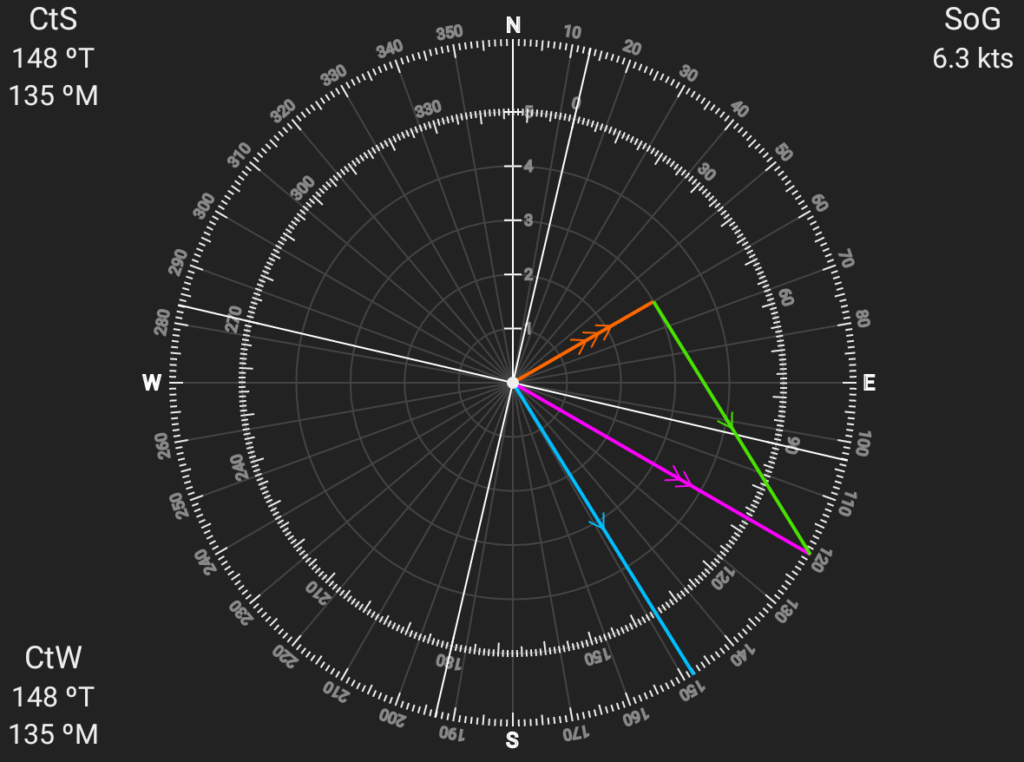
Draw the Course to Steer
Finally, we draw a line from the end of the current line back to the track, with its length equal to your boat speed (since that’s how far your boat will move you in an hour). This is the tricky part. It’s crucial to measure the length of this line with your dividers, and then connect it back to the track, NOT to draw the line to the end of the track.
In our example, we’ll once again divide the boat speed by four to keep the lines shorter, so we’ll end up with a line length of 1.5nm (6 knots / 4).
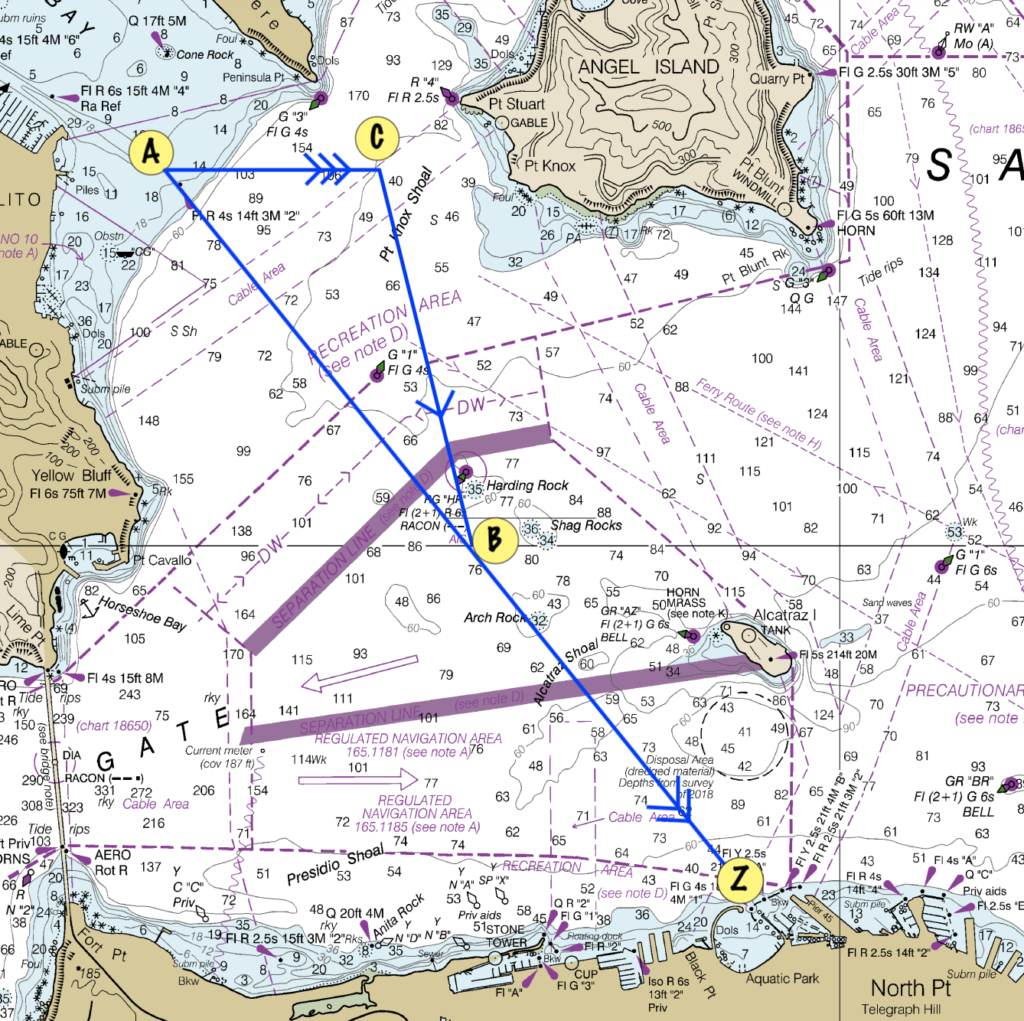
The line we just drew is our Course to Steer. We once again use the plotter to transfer this line to the compass rose, and we end up with a CtS of 151ºT. We measure the length from our starting point (A) to the end of our CtS (B) to get our Speed over Ground (SoG), which turns out to be 7.4 knots. This seems correct intuitively since our boat speed is 6 knots and the current will be helping us along our way.
Doing the Math
NavCalc calculates CtS and SoG using math instead of dividers and plotters. The idea is the same, but instead of measuring things out, we’ll use the Law of Sines.
To start, think about the triangle that we drew above:
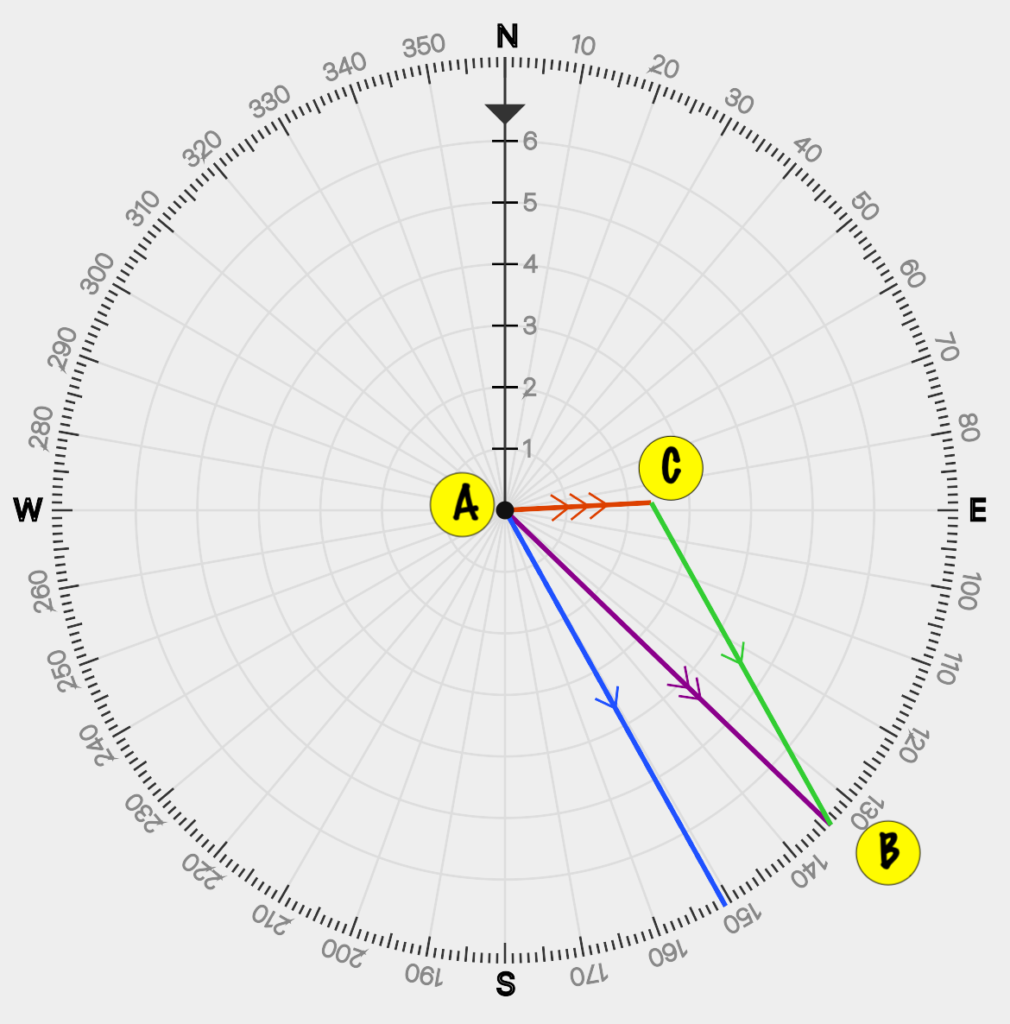
We have our starting point, A, the point our current takes us in a quarter hour, C, and the point our boat takes us to in a quarter hour, B.
The line AB runs along our Track towards our destination. The line AC is the current vector. The line CB is our Course to Steer.
Here’s what we know from our example above:
- Our desired heading (the direction of AB) is 134ºT
- Our boat speed (the length or magnitude of BC) is 6.0 knots
- The direction or set of the current (the direction of AC) is 87ºT
- The current’s speed or drift (the length of AC) is 2.38 knots
What we don’t know is what we need to solve for:
- The Course to Steer (the direction of CB)
- Our Speed over Ground (SoG) or velocity made good (the length of CB)
Let’s pop those into our diagram:
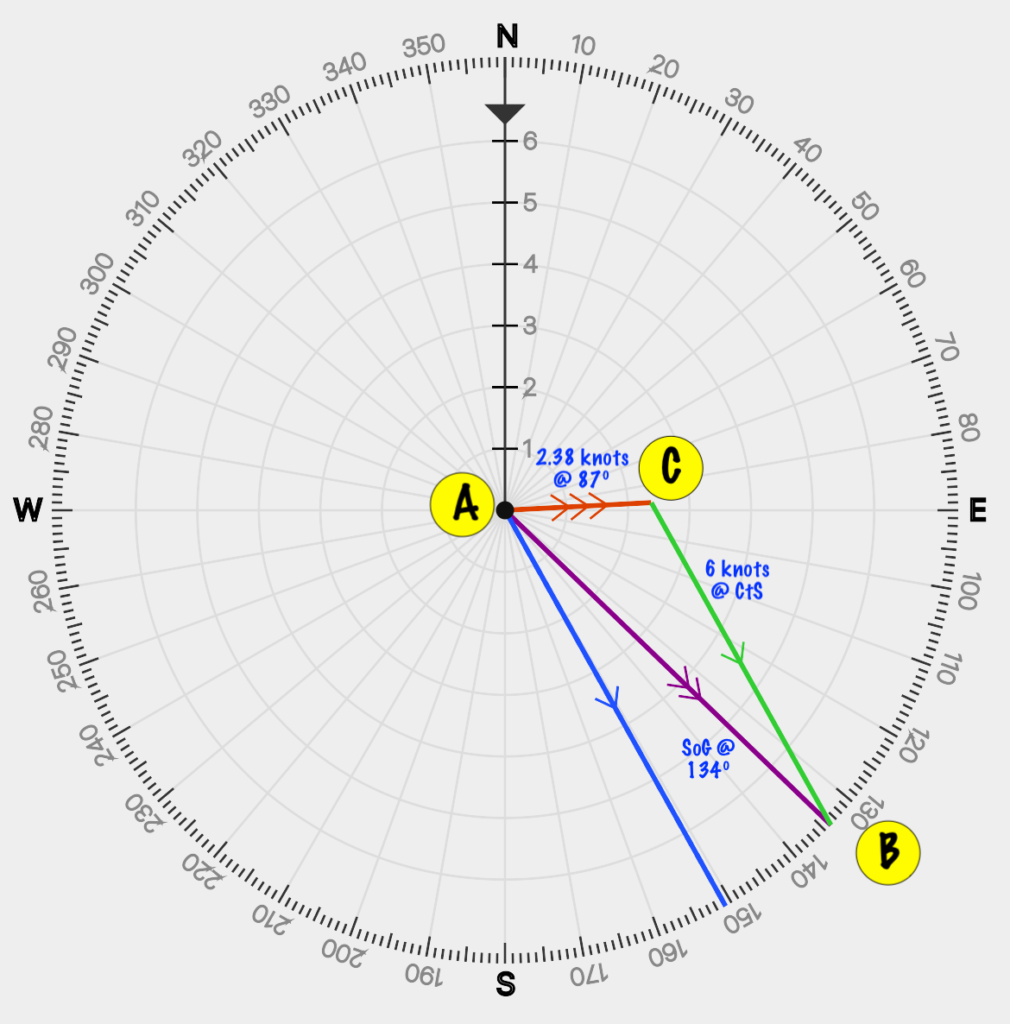
Now, imagine that we label each angle in the triangle using the same names as the points, A, B, C. So, A is the angle between the track (line AB) and the current vector (line AC).
To start, we trivially calculate the angle between our heading and the current vector:
A = heading - current set
A = 134 - 87
A = 47Now we can use the Law of Sines, which states that, in any triangle, the ratio of the Sine of each angle to it’s opposite side will be a constant. In other words:
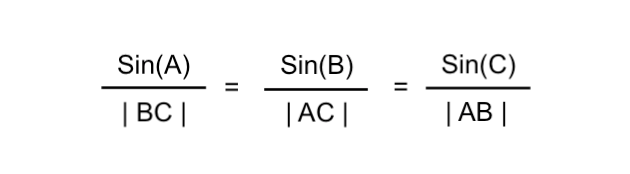
We know A (we just calculated it above) and we know |BC|, which is the boat speed. We also know |AC|, which is the current’s drift. We can now solve for B, which is the angle between the track’s end point and the current’s end point.
We can also trivially solve for the last angle, C.
B = asin(sin(A) * len(AC) / len(BC))
B = asin(sin(47º) * 2.38/ 6)
B = 17
C = 180 - A - B
C = 116To put this back into the language we care about, we can now find our Course to Steer by adding the angle B to the Heading:
CtS = 134 + 17
CtS = 151We can also compute our Speed over Ground (the length of vector AB) by once again applying the Law of Sines:
AB = len(BC) * sin(C) / sin(A)
AB = 6 * sin(116) / sin (47)
AB = 7.4 knotsAnd that’s it!
We’ve mathematically solved for our CtS of 151º and our speed made good of 7.4 knots, which, thankfully, matches the results we got with our chart, plotter, and dividers.
By, the way, I’ve done this particular sail many times with a typical flood current of 2-3 knots, and this is exactly how it works. To get to Aquatic Park, you must aim significantly farther West of the entrance (that is, more towards the Golden Gate Bridge).
When I’m sailing, I get a sense of the current set and drift by ranging on objects ashore, like the entrance to Aquatic Park, and I adjust my course accordingly. I also use Navionics to show me the difference between my heading and my course. But it’s nice to know I could calculate it all if need be!